Introduction to Matrix, it's basic operations and using Universal Calculator app for Matrix Operations.

Download the Universal Calculator App for Android.

Launch the App(mobile only) : Universal Calculator.

Introduction

In mathematics, A matrix is an arrangement of elements (numbers, symbols etc.) in the form of rows and columns.
A matrix is generally denoted by enclosing the matrix name within square brackets as shown below.

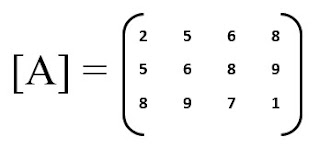
In the example given above, A is a matrix of order(dimension) 3 x 4 as it has three rows and 4 columns.
Each element of a matrix is generally identified by using row and column numbers as its subscript, e.g. shown below.

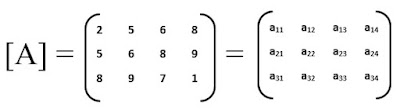
a₁₁=2, a₁₂=5, a₁₃=6, a₁₄=8
a₂₁=5, a₂₂=6, a₂₃=8, a₂₄=9
a₃₁=8, a₃₂=9, a₃₃=7, a₃₄=1

Matrices from a pure mathematical perspective represent linear algebraic functions, called vector space (we will get into detailed explanation of this statement in future articles).

Matrices (Plural for matrix) and its properties are used in many applications such as solving System of linear equation, computer graphics etc.

Mathematical operations in matrix:

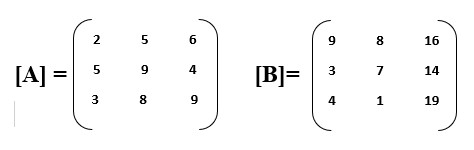
1) Addition: Matrices can be added only when their dimensions are same.
E.g.: consider matrix [A] and matrix [B] below, the sum of these two matrices ([S]) is obtained by simply adding corresponding elements of the two matrices.

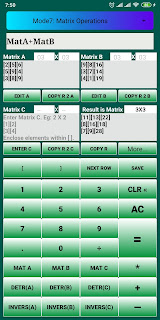
Matrix Addition in Universal Calculator :
Open calculator, switch to “Matrix Operations” mode, enter matrices [A] and [B] and save. enter equation MatA+MatB and click on the Result.
Below screenshot for reference.

Download the android App at play store UniversalCalculator.

Launch the App(mobile only) : Universal Calculator.

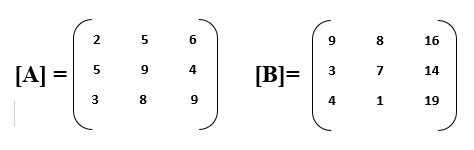
2) Subtraction: Subtraction in matrix is also possible only when dimension of both matrices are same.
E.g.: consider matrix [A] and matrix [B] below, the difference/subtraction([D]) of these two matrices is obtained by simply subtracting corresponding elements of [B] from corresponding elements of the [A].

Matrix Subtraction in Universal Calculator :
Open calculator, switch to “Matrix Operations” mode, enter matrices [A] and [B] and save. enter equation MatA-MatB and click on the Result.
Below screenshot for reference.

Download the android App at play store UniversalCalculator.

Launch the App(mobile only) : Universal Calculator.

3) Matrix Multiplication: Multiplication in matrix operations is of two type.

3.a) Multiplication of a matrix by a scalar: multiplication of a matrix with scalar such as real numbers is simply obtained by multiplying each element of matrix with scalar.
E.g.: if [A] is a matrix then multiplication of this matrix with a scalar number 3 yields another matrix([M]) whose elements are simply obtained by multiplying all element of [A] with 3.

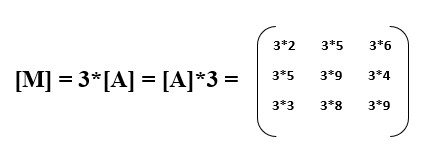
Note that the dimension of the resultant matrix remains unchanged.

3.b) Multiplication of a Matrix with another matrix: Two matrices [A]and [B] can be multiplied if and only if the number of columns of first matrix is same as the number of rows of second matrix.
If [A] is matrix of order m x n and [B] is a matrix of order p x q , then [A]*[B] exists only if n = p, and the resultant matrix(R) will have dimension m x q.
The resultant matrix is obtained by multiplying rows of matrix [A] with columns of Matrix [B].

Note : please note that in matrix operations the result of [A]*[B] is not always same as [B]*[A],
i.e. [A]*[B] != [B]*[A], 

Consider the Example below:

Matrix Multiplication in Universal Calculator :
Open calculator, switch to “Matrix Operations” mode, enter matrices [A] and [B] and save. enter equation MatA*MatB and click on the Result.
Below screenshot’s for reference.

Download the android App at play store UniversalCalculator.

Launch the App(mobile only) : Universal Calculator.

4) Matrix Division: Like Matrix multiplication, matrix division also has two categories.

4.a) Matrix Division by Scalar: division of a matrix with scalar such as real numbers is simply obtained by dividing each element of matrix with the given scalar number.
E.g. if [A] is a matrix then multiplication of this matrix with a scalar number 3 yields another matrix([D]) whose elements are simply obtained by multiplying all element of [A] with 3.

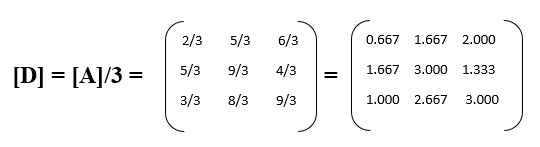
Note:
a. that a matrix can be divided by a scalar, but a scalar cannot be divided by a Matrix.
b. Dimension of the resultant matrix remains unchanged.

4.b) Division of a matrix by a matrix: It is not possible to divide a matrix by another; however, we have a similar concept.
recall that if x and y are real numbers then:
x/y = x*1/y, where 1/y could be called as inverse of y since y*y^-1=y^-1*y = 1
therefore, x/y = x*y^-1.

Similarly, if we have two matrices [A] and [B], then [A] / [B] = [A]*[B]^-1.

The [B]^-1 is defined such that,
[B][B]^-1 = [B]^-1[B] = [I], where I is and identity matrix (A square matrix whose diagonal elements are all 1 and all other elements are 0).
The inverse of a matrix is obtained by dividing adjoint of the matrix by its determinant.
Therefore if [A] is a matrix then:

A^-1 = adj.(A) / |A|

Both finding determinant of a matrix and adjoint of a matrix are separate topics in themselves, therefore we will not be discussing them in detail here. We shall have a separate article for the same.

From the above discussion we can derive the following very important points:
1. For division to exist, it must be possible to find the inverse of the divisor matrix.
However, Inverse is defined only for square matrices whose determinant is not zero.
Hence the divisor matrix must be a square matrix whose determinant is not equal to zero.
2. The number of columns of dividend matrix must be equal to number of rows of divisor matrix.
Below is an example of matrix division using 2x2 divisor matrix.


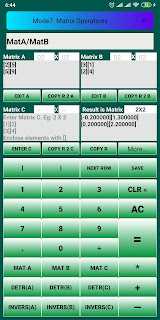
Matrix Division in Universal Calculator :
Open calculator, switch to “Matrix Operations” mode, enter matrices [A] and [B] and save. enter equation MatA/MatB and click on the Result.
Below screenshot for reference.

Download the android App at play store UniversalCalculator.

Launch the App(mobile only) : Universal Calculator.

Thank you for your interest.

We should go into details of more matrix specific operations in next article.